Số nguyên tố là gì? Cách nhận biết và tính chất cơ bản

Trong thế giới toán học rộng lớn và đầy bí ẩn, có những con số tuy nhỏ bé nhưng lại mang trong mình sức mạnh đặc biệt — đó chính là số nguyên tố. Từ những bài học đầu tiên về số học đến các ứng dụng phức tạp trong mật mã học, khoa học máy tính hay trí tuệ nhân tạo, số nguyên tố vẫn luôn đóng một vai trò nền tảng và không thể thay thế. Chúng được ví như những “viên gạch nguyên thủy” xây dựng nên tòa nhà đồ sộ của các con số, bởi lẽ mọi số nguyên dương lớn hơn 1 đều có thể phân tích thành tích của các số nguyên tố — một định lý cơ bản nhưng đầy sức nặng.

Tuy quen thuộc trong các bài toán tiểu học, nhưng số nguyên tố lại ẩn chứa vô vàn điều kỳ lạ và thách thức trí tuệ của các nhà toán học qua hàng thế kỷ. Vậy số nguyên tố là gì? Làm sao để nhận biết một số có phải là nguyên tố hay không? Và những tính chất đặc biệt nào khiến chúng trở nên quan trọng đến vậy trong toán học và đời sống? Hãy cùng khám phá câu chuyện thú vị về những con số nguyên tố — nơi những quy luật đơn giản lại mở ra cả một vũ trụ tri thức đầy hấp dẫn.

Số nguyên tố là gì?

1. Định nghĩa

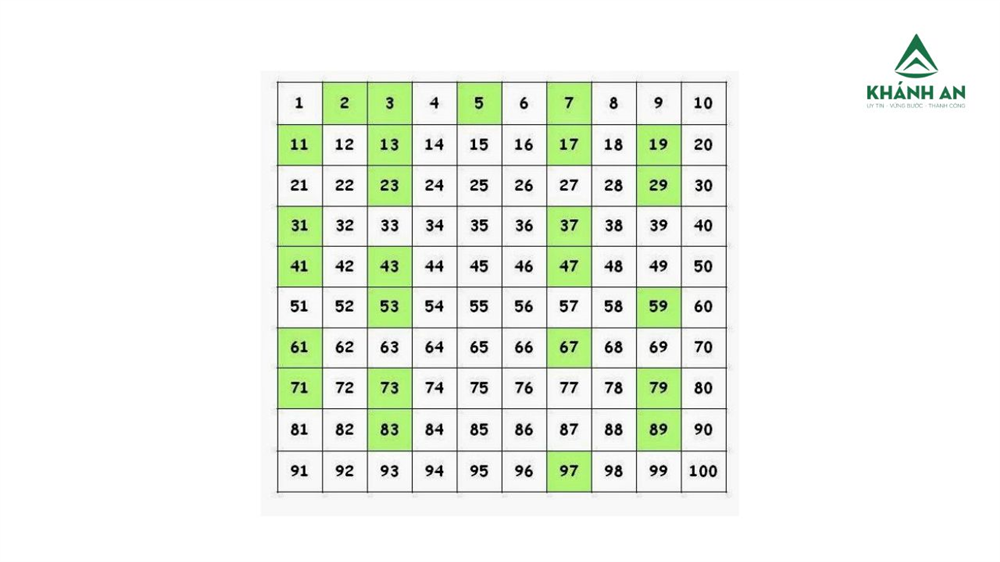
Số nguyên tố là những số tự nhiên lớn hơn 1 chỉ có hai ước số dương phân biệt là 1 và chính nó. Điều đó có nghĩa là một số nguyên tố không thể chia hết cho bất kỳ số tự nhiên nào khác ngoài 1 và chính nó.

Ví dụ:

• 2 là số nguyên tố vì chỉ chia hết cho 1 và 2.
• 3 cũng là số nguyên tố vì chỉ chia hết cho 1 và 3.
• Tương tự, các số như 5, 7, 11, 13, 17,... đều là số nguyên tố.

Đặc biệt, 2 là số nguyên tố chẵn duy nhất. Mọi số chẵn khác đều chia hết cho 2 nên không thể là số nguyên tố.

2. Phân biệt với các loại số khác

a. Số nguyên tố và số hợp

• Số nguyên tố: Chỉ có đúng 2 ước số dương (1 và chính nó).
• Số hợp: Là số tự nhiên lớn hơn 1 có nhiều hơn 2 ước số, tức là ngoài 1 và chính nó, còn chia hết cho ít nhất một số khác.

Ví dụ:

• 7 là số nguyên tố (ước: 1 và 7).
• 8 là số hợp (ước: 1, 2, 4, 8).

b. Số nguyên tố và số nguyên âm, số 1

• Số 1: Mặc dù chỉ chia hết cho 1, nhưng không được coi là số nguyên tố vì nó chỉ có một ước, không thỏa mãn định nghĩa.
• Số nguyên âm: Không được tính là số nguyên tố vì khái niệm số nguyên tố chỉ áp dụng cho số tự nhiên lớn hơn 1.

3. Ý nghĩa trong toán học

Số nguyên tố được ví như “những viên gạch xây nền” cho toàn bộ hệ thống số tự nhiên. Chúng có vai trò đặc biệt quan trọng trong nhiều lĩnh vực:

a. Phân tích số – Thừa số nguyên tố

Bất kỳ số tự nhiên nào lớn hơn 1 đều có thể được phân tích duy nhất thành tích của các số nguyên tố, không kể thứ tự. Đây là Định lý cơ bản của số học.

Ví dụ:

• 30 = 2 × 3 × 5
• 84 = 2² × 3 × 7

b. Trong lý thuyết số

Các định lý nổi tiếng như định lý Fermat nhỏ, định lý Euclid về số nguyên tố vô hạn, hay định lý Wilson… đều xây dựng dựa trên tính chất đặc biệt của số nguyên tố.

c. Ứng dụng trong mật mã học và khoa học máy tính

Số nguyên tố đóng vai trò cốt lõi trong các thuật toán mã hóa hiện đại như RSA, nơi việc phân tích một số lớn thành các thừa số nguyên tố là cực kỳ khó khăn – tạo ra sự bảo mật trong truyền thông số.

Cách nhận biết số nguyên tố

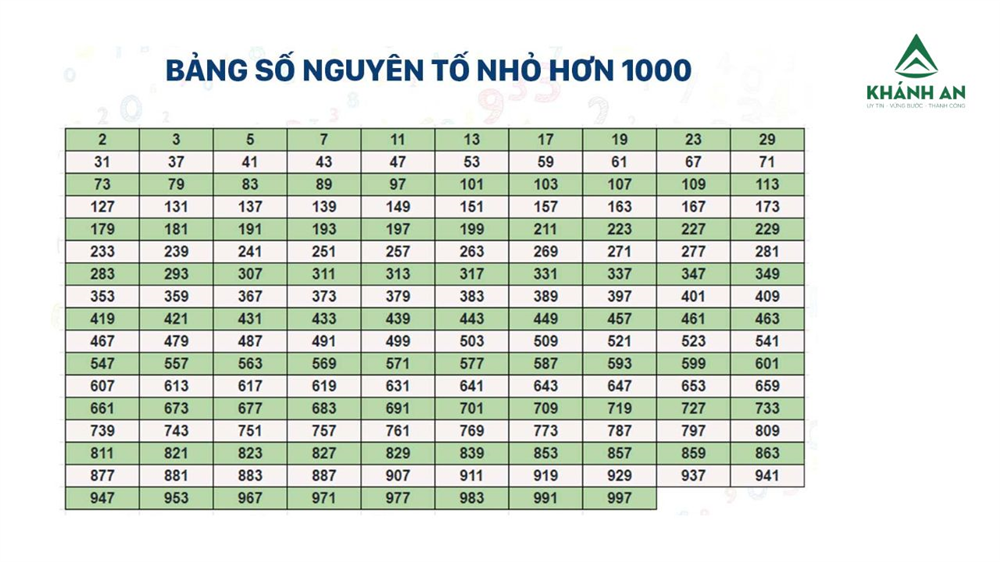
Việc nhận biết một số có phải là số nguyên tố hay không là một kỹ năng cơ bản nhưng quan trọng trong toán học. Tùy theo mục đích và số lượng cần xét, ta có thể áp dụng nhiều cách khác nhau, từ thủ công đến công nghệ hỗ trợ.

1. Cách nhận biết thủ công

Đây là phương pháp phổ thông, thích hợp khi cần kiểm tra từng số riêng lẻ (đặc biệt là các số nhỏ).

a. Nguyên tắc cơ bản

• Một số tự nhiên n lớn hơn 1 là số nguyên tố nếu không chia hết cho bất kỳ số tự nhiên nào nhỏ hơn nó (ngoài 1).
• Tuy nhiên, không cần kiểm tra tất cả các số nhỏ hơn n – chỉ cần kiểm tra các số nhỏ hơn hoặc bằng căn bậc hai của n.

Vì sao?

Nếu n chia hết cho một số lớn hơn căn bậc hai, thì phần còn lại của phép chia sẽ nhỏ hơn căn bậc hai. Nếu không chia hết cho các số từ 2 đến √n, chắc chắn n là số nguyên tố.

b. Ví dụ minh họa

Ví dụ 1: Kiểm tra số 29 có phải là số nguyên tố không?

• √29 ≈ 5.38 ⇒ chỉ cần kiểm tra chia hết cho các số: 2, 3 và 5.
• 29 không chia hết cho 2 (số lẻ), không chia hết cho 3 (29 ÷ 3 ≈ 9.67), không chia hết cho 5 (không tận cùng là 0 hoặc 5).

 → Kết luận: 29 là số nguyên tố.

Ví dụ 2: Kiểm tra số 35

• √35 ≈ 5.91 ⇒ kiểm tra các số: 2, 3 và 5.
• 35 là số lẻ → không chia hết cho 2
• 35 ÷ 3 ≈ 11.67 → không chia hết cho 3
• 35 ÷ 5 = 7 → chia hết cho 5

 → Kết luận: 35 không phải là số nguyên tố (là số hợp).

2. Dùng sàng Eratosthenes

a. Nguyên lý hoạt động

Đây là một trong những phương pháp cổ điển và hiệu quả nhất để liệt kê các số nguyên tố trong một khoảng nhất định.

Các bước thực hiện:

1. Viết dãy các số tự nhiên từ 2 đến n (ví dụ: 2 đến 100).
2. Bắt đầu từ số nguyên tố đầu tiên là 2. Gạch bỏ tất cả bội số của 2 (tức là 4, 6, 8, 10,...).
3. Chuyển sang số chưa bị gạch tiếp theo (3), rồi gạch bỏ tất cả bội số của nó.
4. Tiếp tục quá trình cho đến khi không còn số chưa bị gạch mà nhỏ hơn hoặc bằng √n.
5. Các số còn lại chưa bị gạch chính là các số nguyên tố.

b. Ưu điểm

• Rất hiệu quả và nhanh chóng khi cần tìm tất cả số nguyên tố trong một khoảng lớn.
• Dễ lập trình và dễ hiểu với học sinh, sinh viên.

Các tính chất cơ bản của số nguyên tố

1. Tính chất toán học

Số nguyên tố không chỉ là một khái niệm cơ bản trong toán học mà còn là nền tảng cho nhiều định lý quan trọng, đặc biệt là trong lý thuyết số. Một trong những tính chất then chốt và nổi bật nhất là:

• Định lý cơ bản của số học: Mọi số nguyên dương lớn hơn 1 đều có thể phân tích duy nhất (không tính thứ tự các thừa số) thành tích của các số nguyên tố. Ví dụ, số 60 có thể được viết thành: 60 = 2 × 2 × 3 × 5

==> Đây được xem là “cấu trúc phân tử” của các số nguyên dương, cho thấy vai trò “nguyên tử” của các số nguyên tố trong thế giới số học.

• Tính vô hạn của số nguyên tố: Vào khoảng thế kỷ thứ 3 TCN, nhà toán học Hy Lạp cổ đại Euclid đã chứng minh rằng số lượng số nguyên tố là vô hạn. Bằng một lập luận phản chứng kinh điển, ông cho thấy rằng cho dù ta có liệt kê bao nhiêu số nguyên tố đi nữa, luôn tồn tại một số nguyên tố mới chưa nằm trong danh sách đó. Tính chất này mở ra một thế giới vô tận để con người khám phá và nghiên cứu.

2. Tính chất đặc biệt của số 2

Trong tập hợp các số nguyên tố, số 2 giữ một vị trí vô cùng đặc biệt:

• Là số nguyên tố chẵn duy nhất: Tất cả các số chẵn lớn hơn 2 đều chia hết cho 2, nên không thể là số nguyên tố. Điều này khiến số 2 trở thành ngoại lệ duy nhất – vừa là số chẵn, vừa là số nguyên tố.
• Từ số 3 trở đi, tất cả số nguyên tố đều là số lẻ: Đây là một hệ quả tất yếu từ định nghĩa số nguyên tố. Nếu một số chia hết cho 2 thì không thể là nguyên tố (trừ chính số 2). Điều này khiến dãy số nguyên tố từ 3 trở lên mang tính chất lẻ liên tục.

3. Ứng dụng trong thực tế

Không chỉ nằm trong sách giáo khoa, số nguyên tố còn có những ứng dụng thực tiễn rất quan trọng, đặc biệt trong lĩnh vực công nghệ và an ninh thông tin:

• Mật mã học: Các thuật toán mã hóa như RSA – một trong những thuật toán bảo mật phổ biến nhất hiện nay – sử dụng tính chất khó phân tích một số lớn thành các thừa số nguyên tố. Chính sự phức tạp trong việc phân tích này giúp tạo ra hệ thống mã hóa an toàn cho dữ liệu cá nhân, giao dịch ngân hàng và thông tin quân sự.
• Công nghệ Blockchain và bảo mật dữ liệu: Sự an toàn trong các giao dịch trên blockchain phần lớn cũng dựa trên các hàm băm (hash function) và thuật toán mã hóa có liên quan đến số nguyên tố. Tính bất khả xâm phạm của dữ liệu trong blockchain đến từ việc không thể tính ngược nhanh chóng – một đặc điểm được xây dựng trên cơ sở lý thuyết số.
• Lý thuyết số và nghiên cứu khoa học máy tính: Trong nhiều thuật toán xử lý số liệu, tìm kiếm, tối ưu và nén dữ liệu, số nguyên tố được sử dụng để tăng hiệu quả và độ chính xác. Chúng là đối tượng nghiên cứu không ngừng của các nhà khoa học trong việc phát triển các hệ thống tính toán mới và nhanh hơn.

KẾT LUẬN

Số nguyên tố không chỉ là một khái niệm trừu tượng trong sách giáo khoa, mà còn là nền móng của rất nhiều lĩnh vực hiện đại: từ việc tạo lập các thuật toán mã hóa dữ liệu, bảo vệ thông tin cá nhân đến việc xây dựng các hệ thống số học tinh vi phục vụ cho khoa học và công nghệ. Với định nghĩa tưởng chừng đơn giản — chỉ là những số tự nhiên lớn hơn 1 và chỉ chia hết cho 1 và chính nó — số nguyên tố lại ẩn chứa sự tinh tế và quy luật kỳ diệu khiến bao thế hệ học giả phải tò mò và đắm say trong hành trình khám phá.

Hiểu được số nguyên tố, cách nhận biết chúng và nắm rõ những tính chất cơ bản chính là bước đầu để mở cánh cửa vào thế giới toán học sâu sắc hơn. Và cũng từ đó, ta càng thêm trân trọng vẻ đẹp logic của toán học — nơi mà từng con số, từng định lý đều góp phần tạo nên bức tranh vĩ đại của tri thức nhân loại. Hy vọng rằng qua bài viết này, bạn không chỉ có thêm kiến thức mà còn khơi dậy niềm hứng thú với những điều kỳ diệu ẩn trong các con số tưởng chừng bình thường nhất.

Giới thiệu về dịch vụ Công ty tư vấn Khánh An

Khánh An tự hào là một trong những đơn vị uy tín cung cấp dịch vụ luật tại Việt Nam. Chúng tôi cam kết mang đến cho Quý Khách hàng các giải pháp pháp lý toàn diện và hiệu quả, đáp ứng đầy đủ nhu cầu và yêu cầu của từng doanh nghiệp cũng như cá nhân.

Các lĩnh vực tư vấn của chúng tôi bao gồm:

• Tư vấn và cung cấp dịch vụ Luật tới doanh nghiệp Việt Nam (bao gồm doanh nghiệp có 100% vốn đầu tư nước ngoài) và các loại giấy phép con.
• Tư vấn cho các Doanh nghiệp Việt Nam đầu tư sang các thị trường Singapore, Hồng Kông, BVI,...
• Tư vấn hoàn thiện Hợp đồng, các văn kiện pháp lý cho Doanh nghiệp.

Giá trị cốt lõi của Khánh An

Chúng tôi luôn hướng tới 3 giá trị cốt lõi: UY TÍN – CHẤT LƯỢNG – HIỆU QUẢ CAO. Những giá trị này không chỉ là kim chỉ nam trong hoạt động của chúng tôi mà còn là động lực để chúng tôi không ngừng phát triển. Chúng tôi tự hào khi nhận được những phản hồi tích cực từ Quý Khách hàng, điều này khẳng định chất lượng dịch vụ mà chúng tôi cung cấp.

Khánh An sẽ tiếp tục nỗ lực hết mình để mang đến dịch vụ luật tốt nhất, đồng hành cùng sự phát triển bền vững của Quý Khách hàng.

Thông tin liên hệ:

CÔNG TY TNHH TƯ VẤN KHÁNH AN

Website: https://khanhanlaw.com/

Địa chỉ:Toà nhà 88 Tô Vĩnh Diện, Khương Trung, Thanh Xuân, Hà Nội

Hotline: 02466.885.821 hoặc 096.987.7894.

Email: info@khanhanlaw.net

Xem thêm: Thủ tục thành lập Viện nghiên cứu khoa học công nghệ năm 2025